Prince's Blog

0%

KVCache

Posted on In
Symbols count in article: 1.3k Reading time ≈ 5 mins.

这篇文章主要介绍大模型推理技术中的 KV Cache 技术。这项技术的主要目的是为了减少计算量。

Attention

Self-Attention

将 KV Cache 之前，首先需要讲讲自注意力机制。自注意力机制允许将词与其他词关联起来。自注意力机制采取的是查询-键-值（Q-K-V）的形式。

假设有一个序列长度为 6 的句子：「Your cat is a lovely cat」。每个词可以 tokenize 成一个 \(1 \times d\) 的向量。因此这个句子可以被表示为一个 \(A \in \mathbb{R}^{6 \times d}\) 的矩阵。通过可训练的参数矩阵 \(W_K, W_V, W_Q\)，将输入矩阵 \(A\) 利用矩阵乘法表示为 \(K, Q, V\) 矩阵，即： \[ K = A \cdot W_K, \quad W_K \in \mathbb{R}^{d \times d}, \quad K \in \mathbb{R}^{N \times d} \] \[ Q = A \cdot W_Q, \quad W_Q \in \mathbb{R}^{d \times d}, \quad Q \in \mathbb{R}^{N \times d} \] \[ V = A \cdot W_V, \quad W_V \in \mathbb{R}^{d \times d}, \quad V \in \mathbb{R}^{N \times d} \]

经典公式 \(\text{softmax}(\frac{Q \cdot K^T}{\sqrt{d}})\) 捕捉了两个 token 之间的相关性。计算出的矩阵是一个 \(N \times N\) 的相关性矩阵。以上文的句子为例，计算过程如下图所示。\(\text{softmax}\) 的作用就是将每一行的值归一化为 0 到 1 的概率分布，并且每一行的和为 1。训练较好的模型，相同 token 之间的相关性会更高。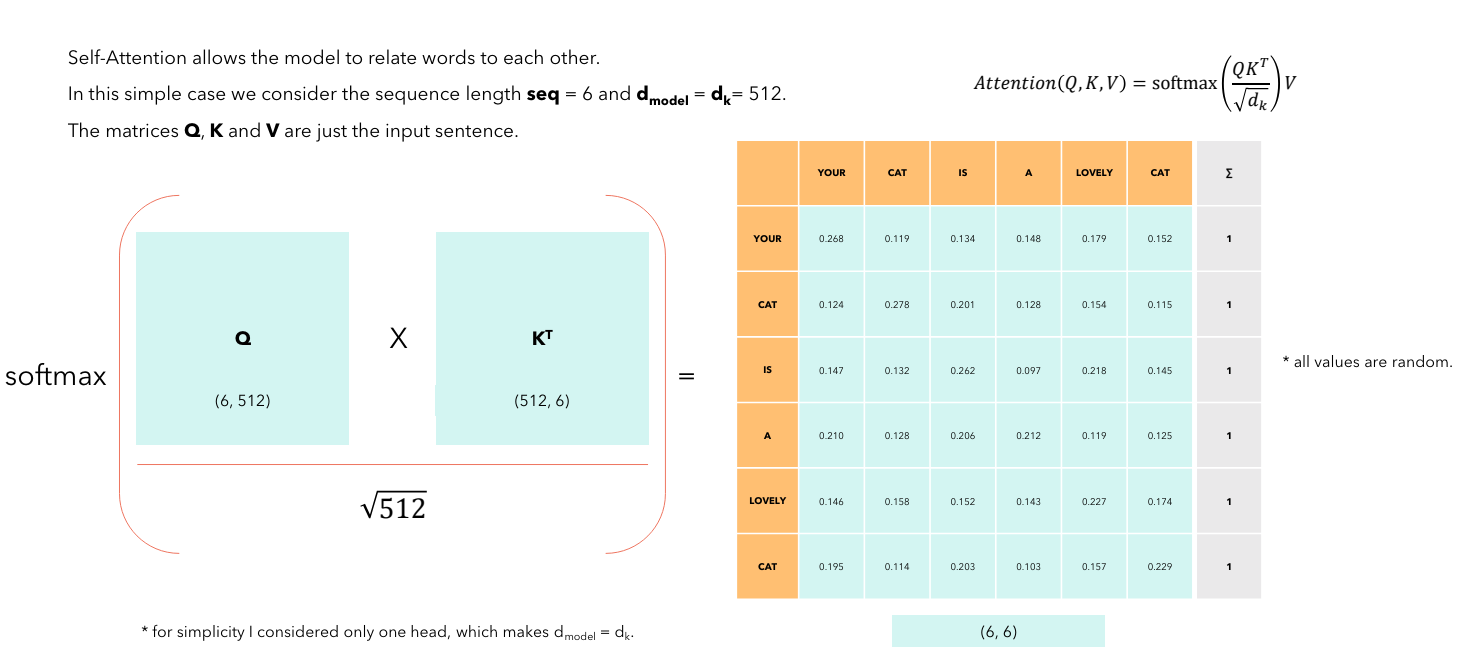

图1. Softmax 矩阵的计算

上一步得到的结果再与 \(V\) 矩阵相乘，即 \(\text{Attention}(K, Q, V) = \text{softmax}(\frac{Q \cdot K^T}{\sqrt{d}}) \cdot V\)，得到与输入矩阵维度相同的输出矩阵。每一行（即经过计算后的新的 embedding）不仅捕捉了词语的含义（由词嵌入表示）或者在句子中的位置（由位置编码表示），还捕捉了每个词和其他词的相互作用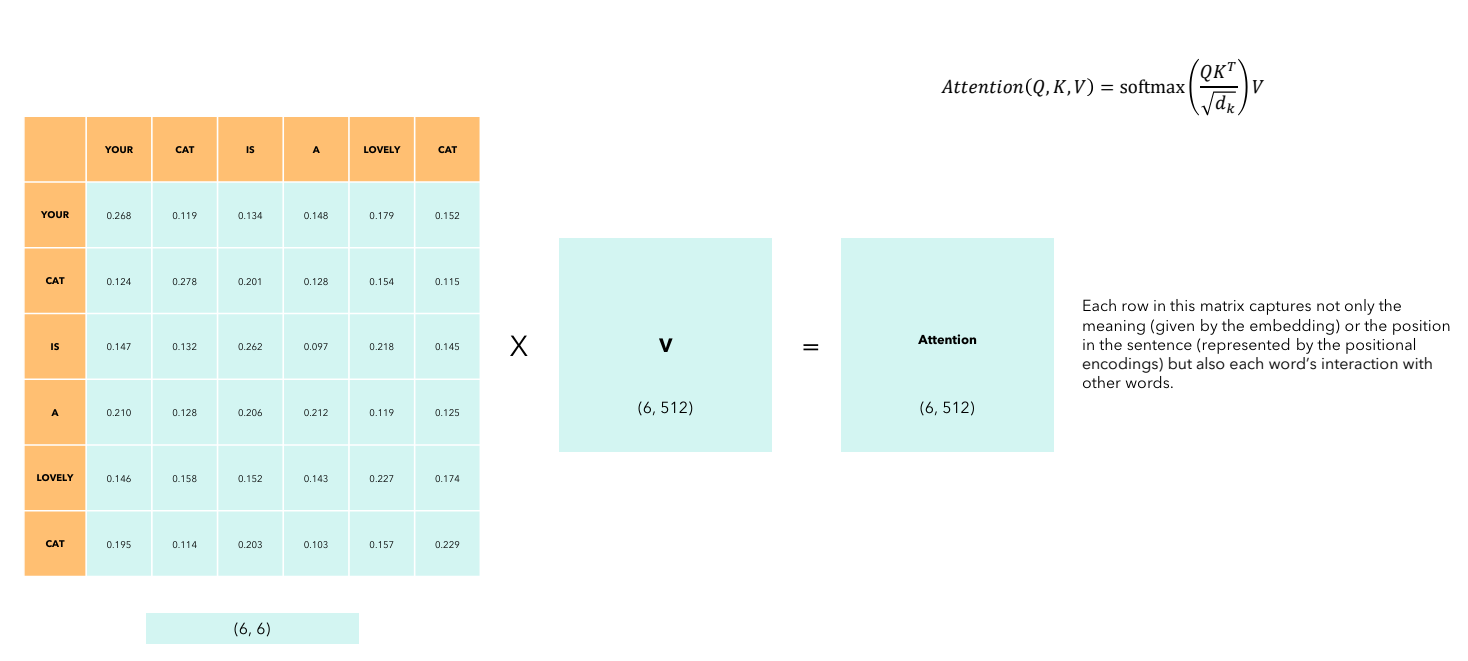

图2. Attention 矩阵的计算

Multi-Head Attention

沿着模型维度 \(d\) 将 \(K, Q, V\) 矩阵分割成较小的矩阵，并且在这些较小矩阵之间计算注意力。所以每一个头都在观察完整的句子，但是是每个 embedding 的不同方面，也就是说我们希望每一个头观察同一个词的不同方面。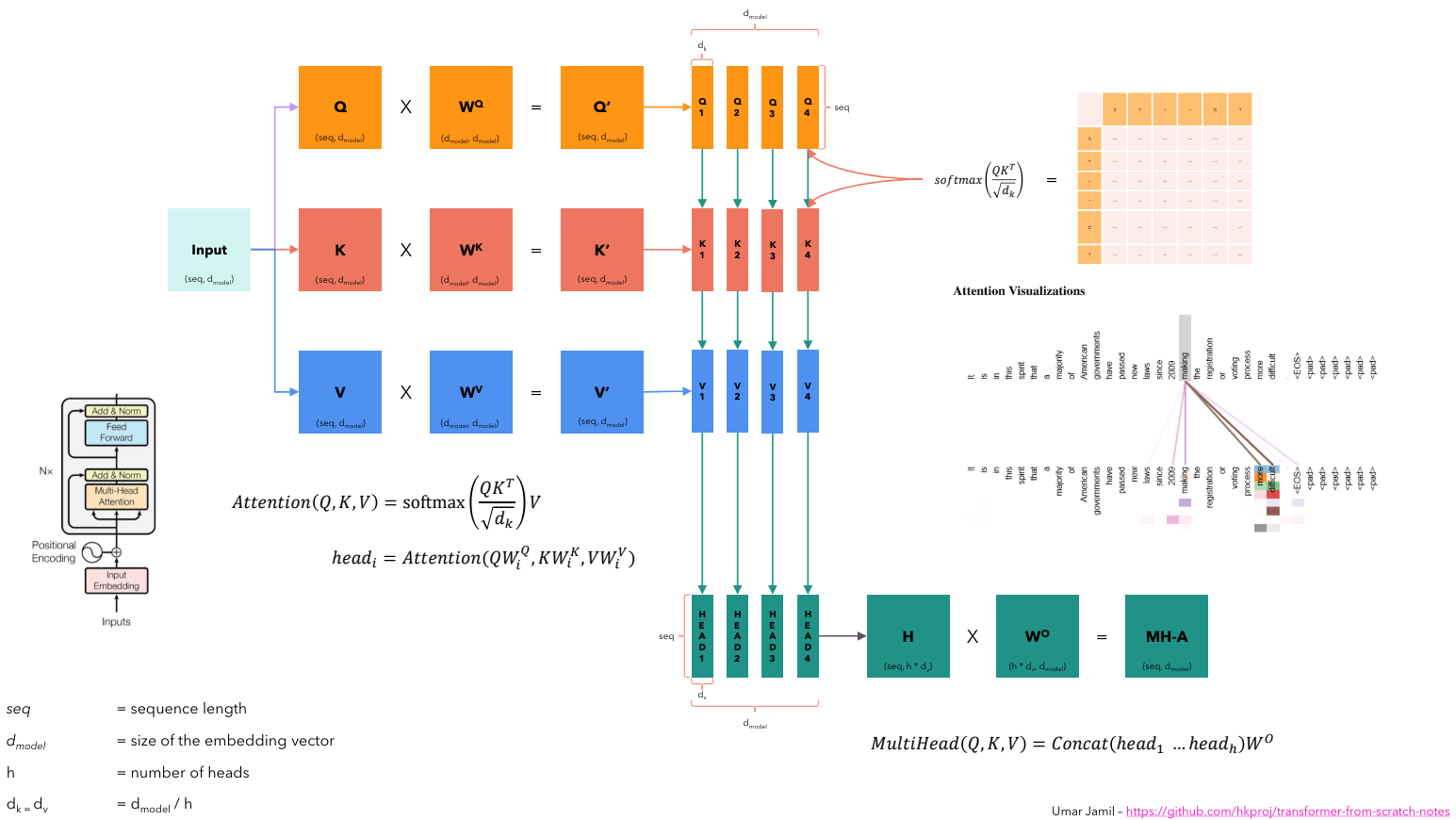

图3. MHA 矩阵计算

KV Cache

原理

在推理的每一步，我们只关心模型输出的最后一个 token。但是模型需要访问之前的所有 token 来决定输出哪个 token。那么有没有办法让模型在推理时对已经看到的 token 减少计算呢？

先来看一个简单的计算 self-attention 的过程（为了方便暂时忽略根号项）：

  • 预测第一个词的时候，计算 Attention 矩阵： \[\text{atten} = \text{atten}_{1} = \text{softmax}(Q_1 \cdot K_1^T) \cdot V_1\]

  • 预测第二个词的时候，\(\text{softmax}\) 按行计算，计算 Attention 矩阵：

\[\begin{split} \text{atten} &= \text{softmax}( \begin{bmatrix} Q_1 \cdot K_1^T & -\inf \\ Q_2 \cdot K_1^T & Q_2 \cdot K_2^T \end{bmatrix} ) \cdot \begin{bmatrix} V_1 \\ V_2 \end{bmatrix} \\ &= \begin{bmatrix} \text{softmax}(Q_1 \cdot K_1^T) & -\text{softmax}(\inf) \\ \text{softmax}(Q_2 \cdot K_1^T) & \text{softmax}(Q_2 \cdot K_2^T) \end{bmatrix} \begin{bmatrix} V_1 \\ V_2 \end{bmatrix} \\ &= \begin{bmatrix} \text{softmax}(Q_1 \cdot K_1^T) & 0 \\ \text{softmax}(Q_2 \cdot K_1^T) & \text{softmax}(Q_2 \cdot K_2^T) \end{bmatrix} \begin{bmatrix} V_1 \\ V_2 \end{bmatrix} \\ &= \begin{bmatrix} \text{softmax}(Q_1 \cdot K_1^T) \cdot V_1 \\ \text{softmax}(Q_2 \cdot K_1^T) \cdot V_1 + \text{softmax}(Q_2 \cdot K_2^T) \cdot V_2 \end{bmatrix} \begin{bmatrix} V_1 \\ V_2 \end{bmatrix} \end{split}\]

    即： \[ \text{atten}_{2} = \text{softmax}(Q_2 \cdot K_1^T) \cdot V_1 + \text{softmax}(Q_2 \cdot K_2^T) \cdot V_2 \]

  • 以此类推，每一步计算 Attention 矩阵时，只需要当前 token 的 \(Q\) 矩阵。但是 \(K\) 和 \(V\) 矩阵可以复用之前的计算结果。因此需要把每一步的 \(K\) 和 \(V\) 矩阵缓存下来，供之后的计算使用。

下面是一张比较直观的图：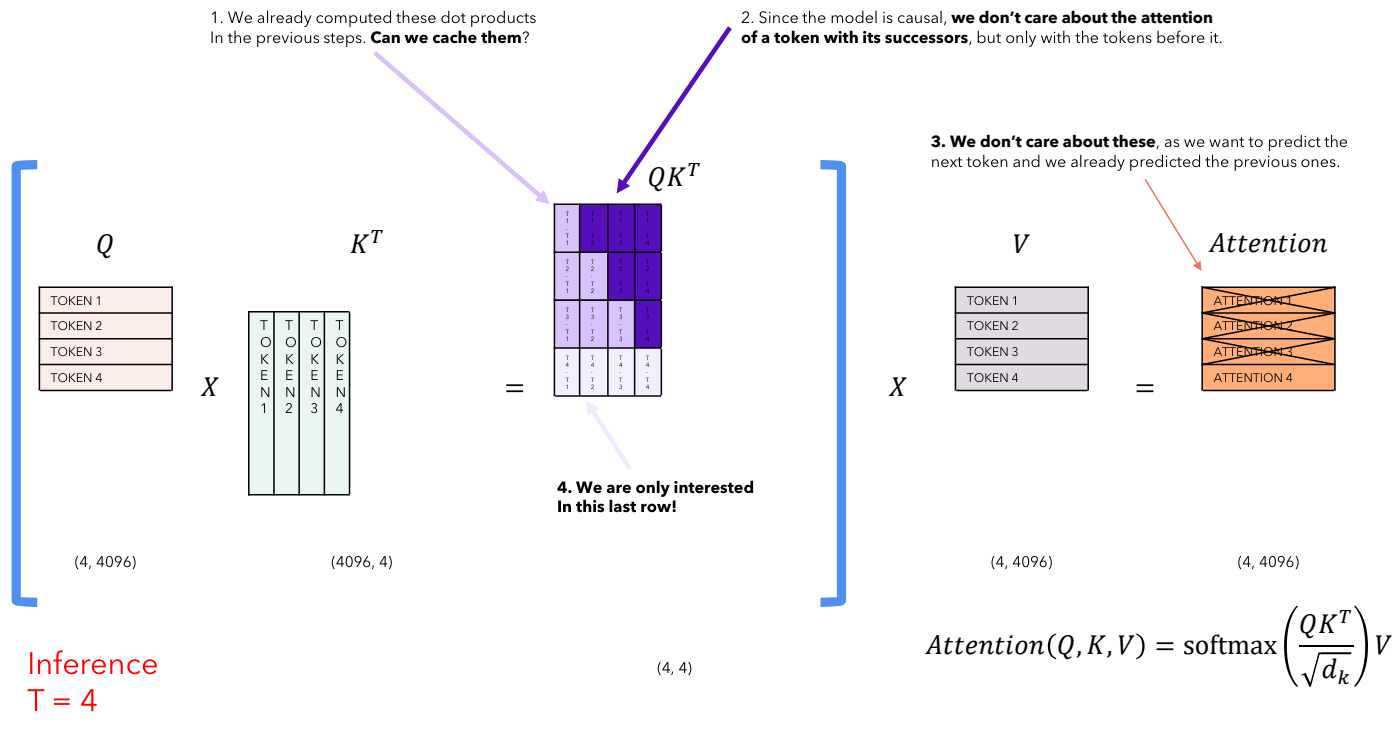

图4. KV Cache 原理

使用KV Cache后推理逻辑的变化

当不使用 KV cache 时，每次生成下一个 token 的注意力计算都会对整条已生成序列（seq_len）进行自注意力计算。

而使用 KV cache 后，在生成新 token 时不需要重新计算所有先前 token 的 Key/Value 表示，只需对当前新生成的 token 计算 Query，并与已缓存的 Key/Value（即 KV cache）进行一次点积操作，得到注意力分布，从而减少计算量。此时，注意力的输出序列长度从整个历史序列长度缩减为 1（仅对当前 token 的预测所需）。

因此, 每层 Decoder 都会接收到一个长度为 seq_len 的张量, 尽管输入的长度为 1，但注意力层并非只对这 1 个 token 做内部计算后结束。因为我们已经缓存了所有之前步骤（token）的 Key 和 Value，因此在注意力计算时，当前生成的 token 的 Query（Q）会与已经缓存的（seq_len-1）个 Key/Value 一起作用，从而模拟完整上下文的自注意力过程。换句话说： - Query 是当前新 token 对应的 Q（长度为1的Q） - Key/Value 则来自于之前缓存的所有历史 token（长度为过去累积的序列长度）

因此，尽管这一轮输入激活只有一个 token，但注意力计算仍然是对所有历史信息进行查询（Q对缓存的K/V），确保模型没有丢失上下文。